终于讲清楚自动驾驶中的坐标变换了...

shuizhonghua

写在前面

本文对线性代数中的坐标变换、基变换两个概念的引入、性质进行了详细推导，并以自动驾驶中的传感器外参标定验证场景举例，介绍了坐标变换和基变换在实际工程中的应用，相信看完本文大家能对坐标变换和基变换有更深的理解。

本文默认读者具备基础的线性代数知识，包括基、线性组合、线性变换等概念。








应用背景

首先引入相机外参，相机外参描述的是车辆系下的三维坐标与相机系下的三维坐标之间的转换关系，用 T来表示， T是一个 4×4的矩阵，左上角 3×3矩阵描述了坐标的旋转，描述了坐标的平移。
车辆系和相机系都是右手坐标系，一般情况下：车辆系的X轴指向车辆前方，Y轴指向车辆左方，Z轴指向天空；相机为前视相机，其坐标系为X轴指向车辆右方，Y轴指向地面，Z轴指向车辆前方。


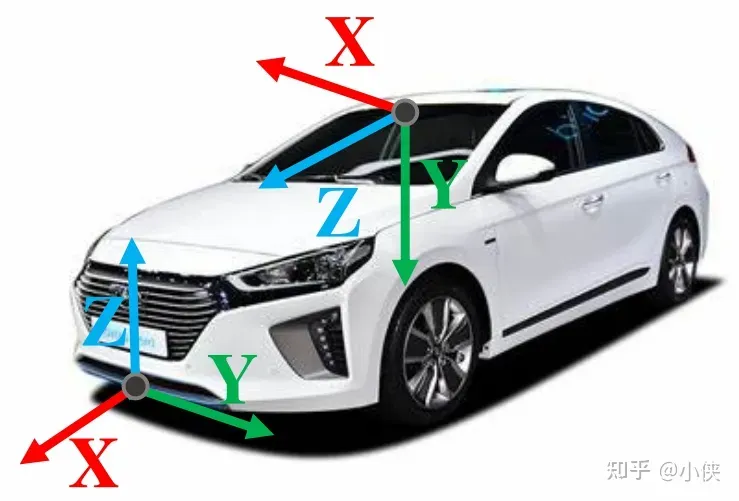
车辆坐标系和相机坐标系
为什么需要坐标转换矩阵T呢，假设我们在图像中检测到一个行人，此时我们可以通过相机内参并结合其他测距传感器，得出该行人在相机系下的位置，但我们并不知道这个人距离车辆有多远，在车辆的正前方还是左前方。因此就需要一个坐标转换矩阵，将相机系下的三维点转换到车辆系下，供下游任务使用。



问题引入

好了，基础应用背景已经介绍完毕，现在步入正题。假设我们已经通过某种标定方法，得到了一个坐标转换矩阵T ，新需求来了，由于前视相机在安装的时候并不像刚才那张图像中一样其Z轴平行于车辆系的X轴，可能会略微偏向天空、地面，也有可能偏向左侧（左前视）、右侧（右前视），我现在想看看相机到底偏向哪个方向，即车辆系三个坐标轴如何旋转至相机坐标系。
刚才提到过，坐标转换矩阵T左上角 3×3的矩阵描述了坐标的旋转关系，称其为旋转矩阵R 。
对这个矩阵求逆得到  ，定义好旋转顺序，对  进行分解，可以得到3个按照指定旋转顺序的欧拉角（具体如何分解旋转矩阵可以参考[1]），这3个按照指定旋转顺序的欧拉角就描述了如何将车辆系旋转至相机系。
先总结一下我们的结论：外参是坐标变换矩阵，左乘车辆坐标系下的三维点得到相机坐标系下的三维点；外参左上角3×3矩阵块的逆是基变换矩阵，对其进行欧拉角分解可以得知如何从车辆坐标系旋转到相机坐标系。
为什么要对 进行分解才能得知如何从车辆坐标系旋转到相机坐标系？为什么这么巧刚好是  ？先别懵，我们先验证这个结论对不对，再来解释为什么。



实验验证

为了实验能更加直观和真实，我们先做出如下设置：

车辆坐标系原点设置在车辆前保险杠的中心处，车辆系的X轴指向车辆正前方，Y轴指向车辆正左方，Z轴指向天空；
将相机系原点设置在挡风玻璃后的上方处，相机系的X轴指向车辆正右方，Y轴指向地面，Z轴指向车辆正前方，相对于车辆坐标系的原点，相机系原点相对于相机系X、Y、Z方向上的平移分别为-1.25、0.1、0.65，直观理解为相机位于车辆前保险杠的后上方，并且偏左一点点；
车辆系前保险杠前方有一个行人，其中心点相对于车辆系X、Y、Z方向上的平移分别为1、-0.2、0.6，即该行人在车辆坐标系下的坐标为 ，直观看就是这个行人在车辆的右前方。上述位置关系如下图所示：

车辆、相机与人的位置关系
假设我们事先通过标定，已经知道了坐标转换矩阵  。


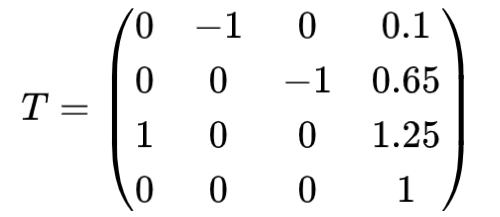
那么车辆坐标系下的一个三维点 ，， 在相机坐标系下的位置计算如下所示，结合图中的位置关系不难验证计算正确。



关键的地方来了，按照上一部分文章所述，我们取坐标转换矩阵 T左上角的3×3矩阵，并对其求逆，得到



我们采用Eigen对旋转矩阵  进行分解，按照X、Y、Z轴的顺序得到3个欧拉角0°、90°、-90°，旋转方式为内旋，即绕着旋转后的自身相应轴进行旋转。
#include <eigen3/Eigen/Core>
int main(){
  float pi = 3.14159265358979;
  Eigen::Matrix3f R_inv;
  R_inv << 0, 0, 1, -1, 0, 0, 0, -1, 0;
  Eigen::Vector3f euler_angle = R_inv.eulerAngles(0, 1, 2); // 0: X轴，1: Y轴，2: Z轴，前后顺序代表旋转顺序，旋转方式为内旋
  std::cout << "先绕X轴旋转: " << euler_angle[0] * 180 / pi <<std::endl;
  std::cout << "再绕Y轴旋转: " << euler_angle[1] * 180 / pi << std::endl;
  std::cout << "最后绕Z轴旋转: " << euler_angle[2] * 180 / pi << std::endl;
}
// Console Output:
// 先绕X轴旋转: -0
// 再绕Y轴旋转: 90
// 最后绕Z轴旋转: -90

按照先绕X轴0°，再绕Y轴90°，最后绕Z轴-90°的顺序，将车辆坐标系旋转至相机坐标系，可以看出与我们设想的情况一致，验证完成。感兴趣的读者可以采用上述代码对R进行分解，能看到采用R分解出的欧拉角对车辆坐标系进行旋转后与实际情况不符。

车辆坐标系->相机坐标系
OK，至此我们已经验证，如果要将车辆坐标系旋转至相机坐标系，需要先对坐标变换矩阵 T中左上方 3×3的旋转矩阵R求逆，再进行欧拉角分解，得到的就是车辆坐标系如何旋转至相机坐标系。
在不考虑平移的情况下，坐标变换矩阵 T 中只包含 R ，因此我们也可以称 R 为坐标变换矩阵，其描述了坐标间的变换关系；我们将成为基变换矩阵，其描述了坐标系之间的变换关系。
我们接下来采用线性代数，来分析为什么坐标变换矩阵和基变换矩阵刚好就是互为逆的关系。





线性代数解释




（坐标变换和基变换的本质）


对  中的一组旧基  进行线性组合，可以变为一组新基  ， 如下式所示。注意这里每一个基都是  维列向量。
不难验证上述线性组合可以写为下述矩阵乘法的形式，注意这里是右乘矩阵，只有这样才能表示对旧基  进行线性组合。
我们记右乘的这个矩阵为  。还记得我们要做什么吗？重新梳理一下，已知现在有一个点  ，在旧基  下的坐标为  ，现在已知一个线性变换  ，将旧基  变为新基  ，在这组新基下，点  的坐标是多少，应该如何表示？
直接上推导，先把上面的那个公式拿过来：



公式两边同时乘上  （  为  的逆）：



公式两边同时乘上点  在旧基  下的坐标



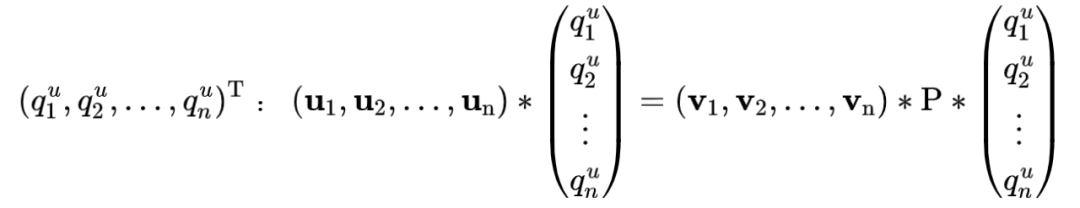
从上面的公式看，答案已经呼之欲出了，可以看到公式右边的形式为新基  乘上一个列向量，该列向量就是点  在新基  下的坐标！即：



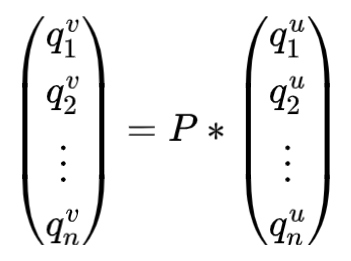
至此，我们可以看到基变换矩阵  通过如下公式描述了两组基之间的变换关系。
坐标变换矩阵P通过如下公式描述了某点Q在两组基下的坐标之间的变换关系。
基变换矩阵和坐标变换矩阵互为逆，推导完毕。



总结

基变换矩阵和坐标变换矩阵的关系之前也在矩阵论这门课中接触过，但当时完全不了解其应用场景，也对为什么这么取名一知半解。直到在实际应用中碰到了这个问题，才发现简简单单的两个公式，在使用时必须根据应用场景对齐进行区分，来选择究竟使用基变换矩阵还是坐标变换矩阵。
感谢各位读者能看到这，有表述不清或者看不懂的地方欢迎评论区里交流。