 在第一篇文章中我们阐述了M圈的含义,以及被测要素带M圈和不带M圈的区别。被测要素带M圈时,其实质就是放宽被测要素公差带。第二篇文章中我们解析了基准带M圈,基准带M圈的实质是基准的公差带可以得到一个位置补偿,换句话说就是零件可以在检具上来回浮动。 本文通过一个具体实例来说明如何解决图纸带M圈的多个零件装配问题。该实例中的公差,同时包含了基准和测量要素带M圈的情况。其具体的装配过程如图1所示,(1)蓝色上壳体的两个定位销与紫色下壳体的两个定位孔装配;(2)蓝色上壳体装配孔与紫色下壳体装配孔通过螺栓连接。我们关注的是在当前公差要求下上下壳体在定位销与定位孔配合后,各个螺栓是否能顺利通过,其装配成功率是多少。对于这种多轴穿多孔问题,常规的尺寸链方法是无法解决的,我们需要借助专业的公差分析软件—DTAS ,利用蒙特卡洛法对其进行仿真分析。
图1
//DTAS多轴穿多孔分析思路 //DTAS模拟上下壳体多孔装配的思路如下,其关键是根据公差如何模拟制造零件及如何模拟孔销浮动。 1、根据图纸公差要求,构造基准模拟体来虚拟制造一定数目的上壳体; 2、根据图纸公差要求,构造基准模拟体来虚拟制造一定数目的下壳体; 3、利用DTAS Floating算法模拟上下壳体之间的浮动,并计算上下壳体各螺栓的通过率及总的通过率。 上壳体模拟制造 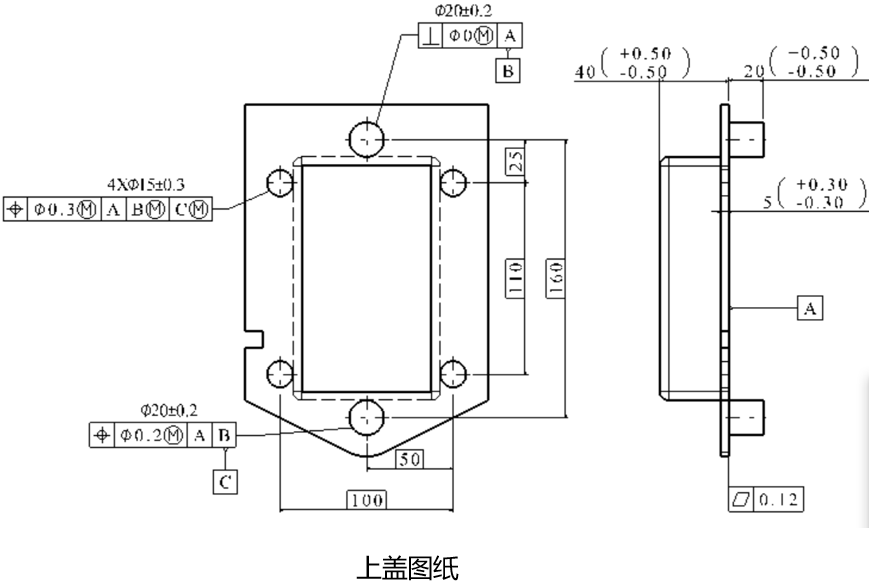  图2 图2 动图2中,上下两个大圆代表上壳的两个定位销,大圆中蓝圈代表公差框中的公差值,大圆中红圈代表补偿后的公差值。由于定位销带M圈,红圈中心可在某些方向上获得一个位置补偿,大圆的圆心始终在红圈内浮动,上下两个大圈公差带中心距始终保持为160mm。大圆两边的四个小圆为四个安装孔,小圆中的蓝圈代表公差框中的公差值,小圆中红圈代表补偿后的公差值。四个小圈中的红圈,水平方向和垂直方向的中心距始终保持为100mm和110mm。四个小圆中红圈中心位置随两个大圆红圈中心位置变动而来回浮动。 下壳体模拟制造 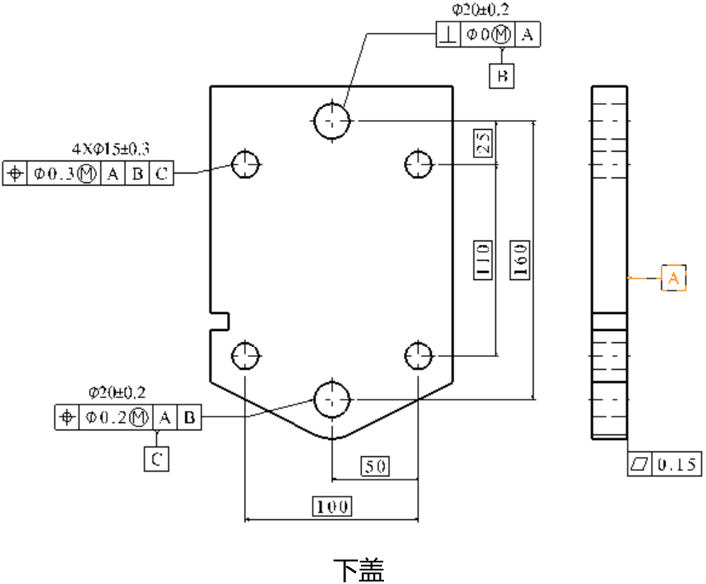 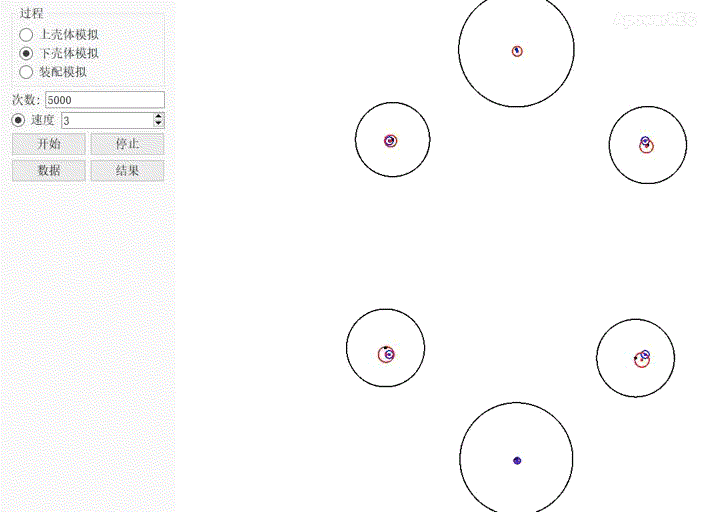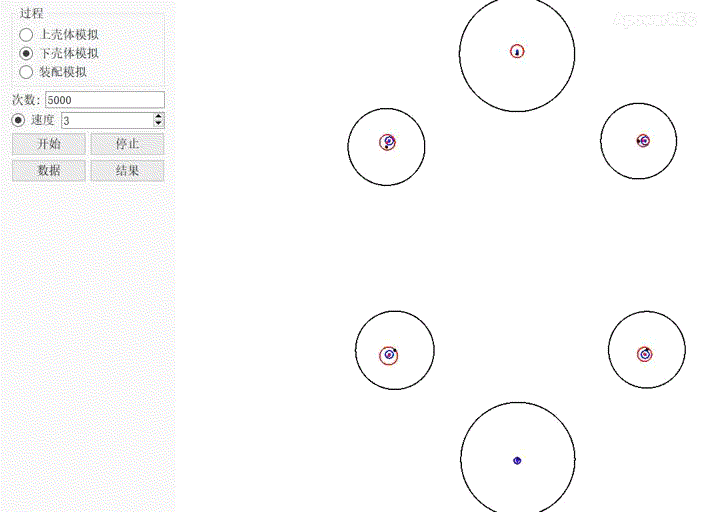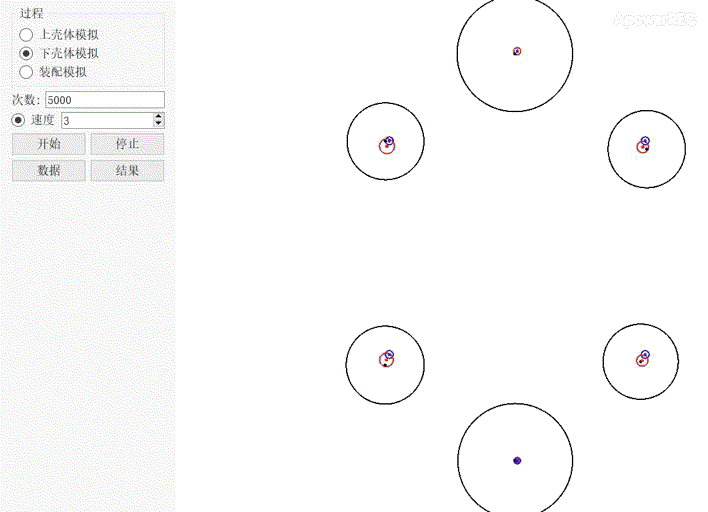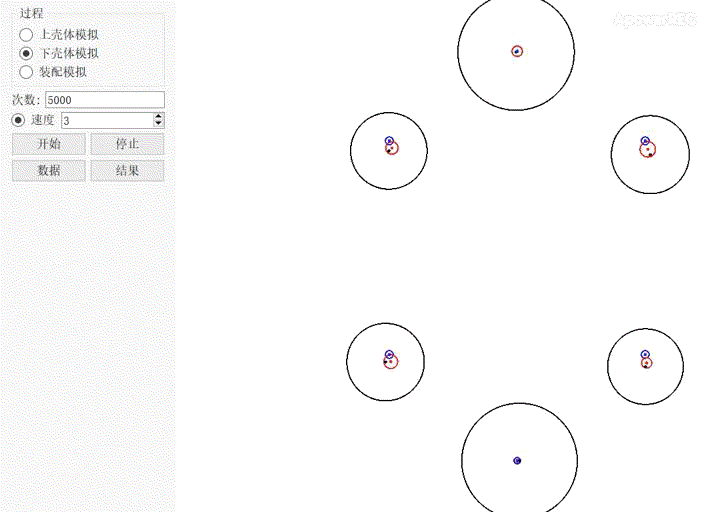 图3 图3 动图3中,上下两个大圆代表上壳体的两个定位孔,大圆中蓝圈代表公差框中的公差值,大圆中红圈代表补偿后的公差值,由于定位孔带M圈,红圈中心可在某些方向上获得一个位置补偿,大圆的圆心始终在红圈内浮动,上下两个大圈公差带中心距始终保为160mm。大圆两边的四个小圆为四个安装孔,小圆中的蓝圈代表公差框中的公差值,小圆中红圈代表补偿后的公差值。四个小圈中的红圈,水平方向和垂直方向的中心距始终保持为100mm和110mm。四个小圆中红圈中心位置随两个大圆红圈中心位置变动而来回浮动。 上壳体、下壳体装配模拟  图4 图4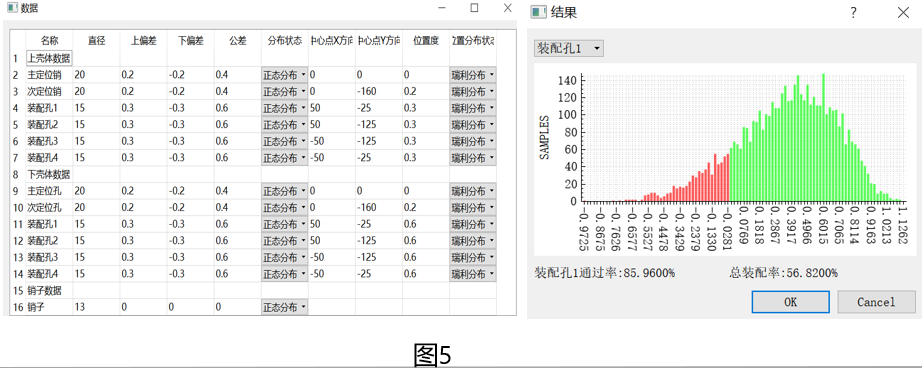 动图4中,上下两个红圈分别代表下壳体的两个定位孔,两个蓝圈分别代表上壳体两个定位销。左右四个红圈分别代表上壳体的四个螺栓装配孔,四个蓝圈分别代表下壳体的四个螺栓装配孔。可以看出由于上壳体销在下壳体孔中有浮动,从而影响周边螺栓孔的对中,并最终影响到螺栓的通过率。DTAS仿真计算结果如图5所示,上下壳体在当前公差下,装配成功的概率为56.82%。
总Lead结 本文是在上两篇文章的基础上用一个实际装配案例来说明M圈在实际公差分析中的应用,该应用过程需要借助专业公差分析软件—DTAS来完成。DTAS软件对图纸中出现的各种M圈均做了充分考虑,并计算出输出总体装配成功率及对应单孔通过率等定量参数,同时还输出零件模拟生产、模拟装配的过程。我们可以通过总装配成功率非常容易的判断当前公差设计的合理性,如不合格,可通过单孔通过率找出问题的根源。
|  |手机版|小黑屋|Archiver|汽车工程师之家
( 渝ICP备18012993号-1 )
|手机版|小黑屋|Archiver|汽车工程师之家
( 渝ICP备18012993号-1 )