matlab计算李雅普诺夫指数方法-jac矩阵方法

wwj557

之前分享过Matlab求解混沌系统最大李雅普诺夫指数

Matlab求解混沌系统最大李雅普诺夫指数

这次分享通过jac矩阵的方法来求解李雅普诺夫指数。

假定研究系统为：某二维非线性动力系统方程组合



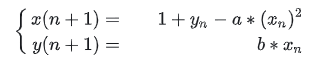
这其jac矩阵的为2*2矩阵，

第一行为x(n+1)分别对xn和yn求导；

第二行为y(n+1)分别对xn和yn求导

则jac矩阵表达式为[-2*a*x,1; b 0]；

完整代码实现：

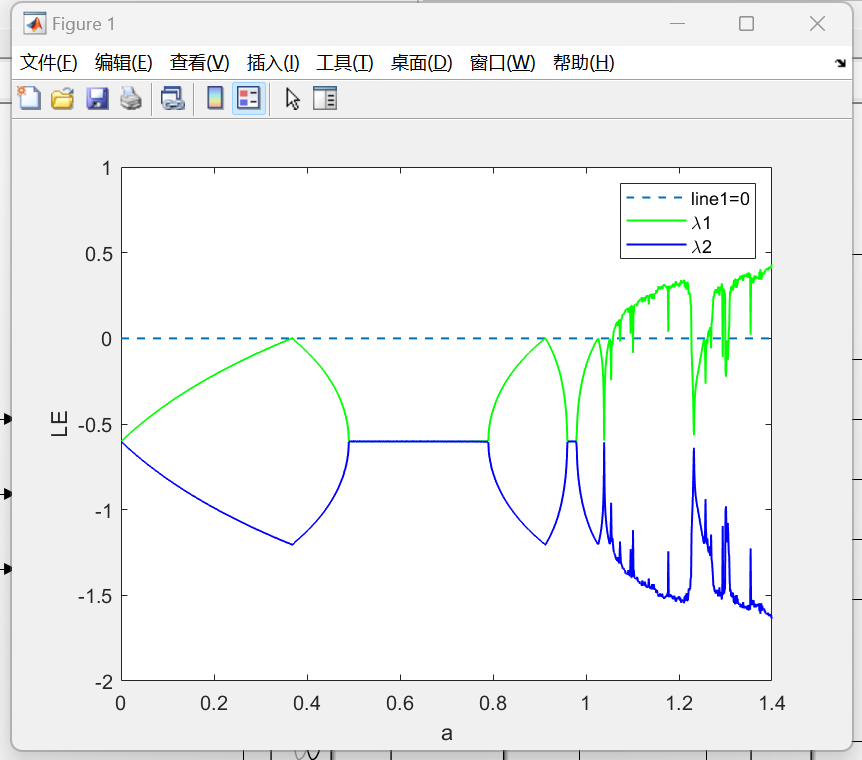
clccloseallclearN = 1000; a = (0:0.001:1.4)'; b = 0.3; na = length(a); LE1 = zeros(na,1); LE2 = zeros(na,1); x = 0.2; y = 0.3; fori = 1:na LCEvector = zeros(2,1); Q = eye(2); forj=1:N xprev = x; yprev = y; x = 1-a(i)*xprev*xprev+yprev; y = b*xprev; Ji = [-2*a(i)*x,1;b 0];B = Ji*Q;[Q,R] = qr(B); LCEvector = LCEvector+log(diag(abs(R))); endLE = LCEvector/N; LE1(i) = LE(1); LE2(i) = LE(2); endfigure(1);plot([0,1.4],[0,0],'--','LineWidth',1);hold onplot(a,LE1,'g',a,LE2,'b','linewidth',1); set(gca,'XLim',[01.4]);set(gca,'YLim',[-21]);legend('line1=0','\lambda1','\lambda2');xlabel('a');ylabel('LE');set(gca,'fontsize',10)

落叶纷飞

作为汽车工程师，对李雅普诺夫指数的计算方法有所了解。对于通过Jac矩阵求解李雅普诺夫指数的方法，其基本步骤包括：确定研究系统的非线性动力方程，计算Jac矩阵，该矩阵由系统状态变量的导数构成。接着，利用Jac矩阵计算李雅普诺夫指数。对于您提到的二维非线性动力系统，Jac矩阵应包括系统变量对自身的导数。具体代码实现涉及矩阵运算及迭代计算。由于您的回复不完整，无法给出详细代码示例。建议补充完整代码及问题细节，以便更准确地为您解答。

[内容由汽车工程师之家人工智能总结，欢迎免费使用，见贴尾]