|
|
汽车零部件采购、销售通信录 填写你的培训需求,我们帮你找 招募汽车专业培训老师
离散系统的基本概念
所谓离散系统,是指系统的输入与输出仅在离散的时间上取值,而且离散的时间具有相同的时间间隔。下面给出离散系统更全面的定义。
【定义】离散系统。凡是满足如下条件的系统均为离散系统:
(1) 系统每隔固定的时间间隔才“更新”一次,即系统的输入与输出每隔固定的时间间隔便改变一次。固定的时间间隔称为系统的“采样”时间。
(2) 系统的输出依赖于系统当前的输入、以往的输入与输出,即系统的输出是它们的某种函数。
(3) 离散系统具有离散的状态。其中状态指的是系统前一时刻的输出量。
离散系统的数学描述
前面给出了离散系统的定义,这里给出离散系统的数学描述,其数学描述应为:

【例1】 对于如下的离散系统模型:

其中系统的初始状态为y(0)=3,系统输入为0,2,4......,则系统在时刻0,1,2……的输出分别为:
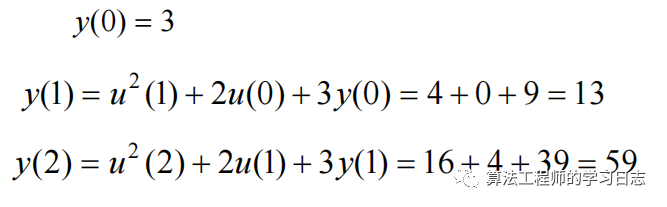
离散系统除了采用一般的数学描述方式之外,还可以采用差分方程进行描述。使用差分方程描述方程形式如下:
设系统的状态变量为x,离散系统差分方程由以下两个方程构成:
状态更新方程:

系统输出方程:

离散系统的Simulink描述
这里以【例1】中的离散系统为例,说明如何利用Simulink对离散系统进行描述,并在此基础上对系统进行简单的分析。此处并不建立系统的Simulink模型进行仿真,而是编写M脚本文件从原理上对离散系统进行说明,并说明离散系统与连续系统的区别之处。
编写脚本文件systemdemo2.m对【例1】中的离散系统进行描述分析:
y(1)=3;% 表示离散系统初始状态为3% 由于MATLAB中数组下标从1开始,这里y(1)相当于上文中的y(0)=3,下同u(1)=0; % 表示离散系统初始输入为0for i=2:11 % 设定离散系统输入范围为时刻0到时刻10 u(i)=2*i; % 离散系统输入向量 y(i)=u(i).^2+2*u(i-1)+3*y(i-1); % 离散系统输出向量endplot(u,y); grid; % 绘制系统仿真结果
系统从时刻0到时刻10的输入与输出的关系如下图所示。其中横坐标表示离散系统的输入向量,而纵坐标表示离散系统的输出向量。说明:这里并没有指定离散系统的采样时间,而仅仅举例说明离散系统的求解分析。在实际的系统中,必须指定系统的采样时间,只有这样才能获得离散系统真正的动态性能。

线性离散系统
对于任何系统而言,系统的描述都可以采用抽象的数学形式来进行描述。这是因为任何系统都可以被看作是输入到输出的某种变换。例如,离散系统可以由下述的变换进行描述:

在离散系统之中,线性离散系统具有重要的地位。下面对线性离散系统进行简单的介绍。在此之前,读者需要理解如下的两个概念:
(1)齐次性:若对于离散系统,如果对任意的输入与给定的任意常数,恒有:

(2) 叠加性:如果系统对于输入和,输出分别为和,恒有:

则称系统满足叠加性。
【定义】线性离散系统:当离散系统同时满足齐次性与叠加性时,即:

则称此离散系统为线性离散系统。
例如,对于如下的离散系统:


线性离散系统的数学描述
对于线性离散系统来说,可以使用最一般的方式对其进行描述,如采用如下的数学方程进行描述:

或采用差分方程进行描述:
状态更新方程:

系统输出方程:

除了使用一般的方式描述线性离散系统之外,针对线性离散系统本身的特点,经常使用Z变换来描述线性离散系统。Z变换是对离散信号进行分析的一个强有力的工具,尤其是对线性离散系统。
Z变换具有多种不同的性质,这里仅介绍Z变换的如下两个性质:
(1) 线性性。所谓Z变换的线性性指的是Z变换满足下面的关系:

(2) 设离散信号 f(k) 的Z变换为 F(z),则 f(k+1) 的Z变换为 z[F(z)-f(0)]。
【例2】 对于如下的线性离散系统:

同时对等式两边进行Z变换,则有:

一般在系统分析中,往往对系统输出与系统输入的比值比较关心,将此式化成分式的形式,有:

在对系统进行描述分析时,此种形式的描述称之为滤波器描述。对上式进行等价变换,可以得到系统的传递函数描述线性系统最常用的一种描述方式:

还可以得到系统的零极点描述:

线性离散系统的Simulink描述
线性离散系统的描述方式有如下四种形式:
(1) 线性离散系统的滤波器模型:在Simulink中,滤波器表示为num=[n0 n1 n2]; den=[d0 d1];其中num表示Z变换域分式的分子系数向量,den为分母系数向量。
(2) 线性离散系统的传递函数模型:在Simulink中,系统的传递函数表示为num=[n0 n1 n2]; den=[d0 d1];
(3) 线性离散系统的零极点模型:在Simulink中,系统零极点表示为gain=K; zeros=[z1, z2]; poles=[0, p1];
(4) 线性离散系统的状态空间模型:在Simulink中,设系统差分方程为如下形式:x(n+1)=Fx(n)+Gu(n);y(n)=Cx(n)+Du(n)。其中x(n), u(n), y(n)分别为线性离散系统的状态变量、输入向量、输出向量。F,G,C,D分别为变换矩阵。在Simulink中,其表示很简单,只需要输入相应的变换矩阵F,G,C,D即可。
【例3】对于如下的线性离散系统:

在MATLAB中输入下面的语句,可以绘制出此系统的Bode图:
>>num=[2 -1 -5];>>den=[1 3 6 2];>>dbode(num,den,1)>>grid;
此离散系统的Bode图如下图所示:

当然也可以用下面的语句求出系统的幅值与相位而不绘制图形:
>>[mag,phase]=dbode(num,den,1);
此外,在MATLAB中,离散系统的不同描述模型之间可以进行相互转化。这里给出几个比较常用的函数:
% 将系统传递函数模型转化为零极点模型[zeros,poles,k]=tf2zp(num,den)
% 将系统零极点模型转化为传递函数模型。% 其中num,den分别为系统的传递函数表示;% zeros,poles,k为系统的零极点模型[num,den]=zp2tf(zeros,poles,k)
至于线性离散系统的状态空间模型描述,这里不再介绍,感兴趣的读者可以参考其它有关的书籍。这里给出它与传递函数模型、零极点模型相互转化的函数命令:
% 将系统状态空间模型转化为零极点模型[zeros,poles,k]=ss2zp(F,G,C,D)
% 将系统零极点模型转化为状态空间模型[F,G,C,D]=zp2ss(zeros,poles,k)
% 将系统状态空间模型转化为传递函数模型[num,den]=ss2tf(F,G,C,D)
% 将系统传递函数模型转化为状态空间模型[F,G,C,D]=tf2ss(num,den)
【例4】 以下面线性离散系统为例说明系统模型的转化。

解:将传递函数模型转化为零极点模型:
>> num=[2 -1 -5];>> den=[1 3 6 2];>> [zeros,poles,k]=tf2zp(num,den)
结果为:
zeros =
1.8508 -1.3508
poles =
-1.2980 + 1.8073i -1.2980 - 1.8073i -0.4039 + 0.0000i
k =
2
将传递函数模型转化为状态空间模型:
>> num=[2 -1 -5];>> den=[1 3 6 2];>> [F,G,C,D] = tf2ss(num,den)
结果为:
F =
-3 -6 -2 1 0 0 0 1 0
G =
1 0 0
C =
2 -1 -5
D =
0 |
|
 |手机版|小黑屋|Archiver|汽车工程师之家
( 渝ICP备18012993号-1 )
|手机版|小黑屋|Archiver|汽车工程师之家
( 渝ICP备18012993号-1 )